The transport matrix obtained from the tracking program
can be used to derive the resolution expected
from the spectrometers.
The horizontal transfer from the vertex to the 
(
) Roman pot is
given by Eq. 1.
where
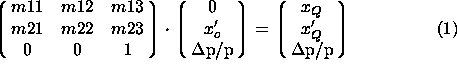is the horizontal position of the particle in the Q pots,
is the angle from the Q to S pots, and
is the initial angle from the interaction point (IP).
The particle's initial conditions at the IP ( and 
)
are reconstructed
from the detector readings ( and ) through the equations:
The transfer matrix parameters from the IP to the () pots are
given below:
m12=9.47(20.2)
m13=23.5(9.02)
m22=-0.345(-0.220)
m23=3.45(1.57)
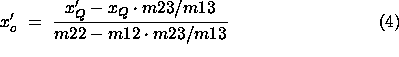
The detector resolutions can be calculated from these equations
using the substitutions 
and
.
The following equations for the resolution are obtained:
The value of 
depends on the point resolution of the detector
and multiple scattering, which are estimated to be about
0.1 mm and 0.04 mm, respectively,
for the detector discussed in Sec. 4.2.1. It is also sensitive
to the uncertainty in the beam position at the location.
The average beam position can be measured very well using elastic events,
and deviations from this position are expected to be about 0.1 mm [38].
Adding these resolutions in quadrature gives 
mm.
This yields estimated resolutions of
and 
.
In practice, the |t| resolution is dominated by the
0.06 mrad angular dispersion
of the beam, which corresponds
to 
.
These resolutions compare well with the expected dipole spectrometer
resolution of 
and
[35].
