Multiple Interactions and Background

  A serious concern about triggering on hard diffraction is the frequency of multiple interactions in the same bunch crossing. There are two types of multiple interactions that are of concern:

1. The superposition of a hard single diffractive event with a minimum bias event.
2. The superposition of a standard single diffractive event with a hard scattering event (pile-up background).

Unlike pile-up (discussed in Sec. 5.3.1), the occurrence of an extra minimum bias interaction in a hard diffractive event is not a background. It does, however, obscure some of the properties of the diffractive events by changing the multiplicity distribution (filling in the rapidity gap) and biasing the energy flow of the event. For high cross section processes we have the luxury of rejecting these events online, and can obtain a good sample of single interaction events in order to properly study the diffractive final states. This can be achieved with single interaction triggers using the upgraded Level Ø detector in a similar manner as in Run I. We would pass the event if there were

• No hits on one side of the Level Ø beam hodoscope scintillators. This is the typical configuration for low to intermediate mass single diffractive events.
• Level Ø hits on both sides, but with a timing consistent with a single interaction hypothesis. Higher mass diffractive events or diffractive events where the interacting parton from the pomeron carries a large fraction of the pomeron momentum will often give hits on both sides of Level Ø.

This single interaction requirement can be implemented at Level 1, so these multiple interaction events will have minimal impact on the bandwidth. The residual multiple interaction contamination in this sample should be small (about 10% from Run I studies) and can be cleaned up further at Level 3 or offline by demanding that the silicon vertex detector find only one primary vertex, which will give a residual contamination of <1%.

The probability P(n=0) of no extra interaction in addition to a hard scattering is easily calculated using the following equations, which give the average number of extra interactions 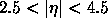in terms of the cross section , instantaneous luminosity 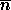, period T, and number of bunches .



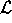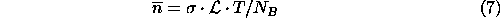
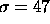The second column in Table 6 (labelled Min Bias) shows the probability of no extra minimum bias interactions as a function of luminosity using a minimum bias cross section of mb, s, and 36 bunches. The single interaction fraction is seen to be quite appreciable at lower luminosities, but falls quickly with luminosity. For rare processes such as diffractive W production it would be undesirable to impose a single interaction requirement at the trigger level, due to the loss in statistics. It is more sensible to read out the Roman pot detectors for all events and just impose single interaction requirements on the higher cross section processes. Of course, there will be an appreciable fraction of rare events with a single interaction that can be studied in more detail.

  
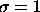
Table 6: Single interaction fraction P(n=0) versus instantaneous luminosity for minimum bias and single diffractive (SD) cross sections, assuming 36 bunches. The probability of two or more extra interactions P(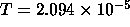) is also given for 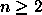mb.

 
• Pile-up Background
• Halo Background