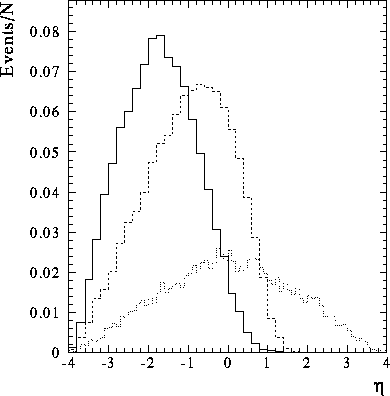
Figure: The pseudorapidity distribution of the two leading (highest
To effectively utilize the large data samples that can be obtained with the FPD (see Sec. 5), it is useful to have Monte Carlo simulations of the physics processes. The Monte Carlo POMPYT [33] incorporates the Ingelman-Schlein model (described in Sec. 2.1.1) and can be used to generate samples to compare to hard diffractive data. The Monte Carlo allows for the choice of different pomeron structure functions and quark and gluon combinations, and can thus be used in conjunction with the data to derive a pomeron structure, or to determine if the concept of a pomeron structure is valid.

Figure: The pseudorapidity distribution of the two leading
(highest ![]() ) jets
for Monte Carlo simulations. The solid (dashed) histogram is
from the POMPYT hard diffractive Monte Carlo with a
scattered proton at
) jets
for Monte Carlo simulations. The solid (dashed) histogram is
from the POMPYT hard diffractive Monte Carlo with a
scattered proton at ![]() and a
soft (hard) gluonic pomeron structure.
The dotted histogram is
from the non-diffractive PYTHIA Monte Carlo.
and a
soft (hard) gluonic pomeron structure.
The dotted histogram is
from the non-diffractive PYTHIA Monte Carlo.
We have performed Monte Carlo studies
of diffractive dijet production.
Figure 7 shows the ![]() distribution of the leading two jets
(
distribution of the leading two jets
(![]() GeV) for three Monte Carlo samples.
The solid and dashed histograms are generated using POMPYT with
soft and hard pomeron structures, respectively, while
the dotted histogram is for a non-diffractive
PYTHIA [34] sample.
This variable clearly has sensitivity to different pomeron structures,
with the softer structure boosted significantly towards negative
GeV) for three Monte Carlo samples.
The solid and dashed histograms are generated using POMPYT with
soft and hard pomeron structures, respectively, while
the dotted histogram is for a non-diffractive
PYTHIA [34] sample.
This variable clearly has sensitivity to different pomeron structures,
with the softer structure boosted significantly towards negative ![]() (the direction opposite the detected proton)
compared to the hard structure and the symmetric
PYTHIA distribution.
This variable and similar variables, such as the longitudinal momentum
of the two jet system (which directly reflects the imbalance between the
parton from the pomeron and the parton from the proton), can be used
to derive the pomeron structure. Event samples of a few hundred events
are adequate to distinguish between a hard and soft structure
(as done in UA8), but larger
samples will allow the detailed extraction of a pomeron structure in various
(the direction opposite the detected proton)
compared to the hard structure and the symmetric
PYTHIA distribution.
This variable and similar variables, such as the longitudinal momentum
of the two jet system (which directly reflects the imbalance between the
parton from the pomeron and the parton from the proton), can be used
to derive the pomeron structure. Event samples of a few hundred events
are adequate to distinguish between a hard and soft structure
(as done in UA8), but larger
samples will allow the detailed extraction of a pomeron structure in various
![]() and |t| bins. These variables, however, cannot distinguish easily
between a quarkonic or a hard gluonic pomeron, which have similar structures.
and |t| bins. These variables, however, cannot distinguish easily
between a quarkonic or a hard gluonic pomeron, which have similar structures.
To derive the quark and gluon content of the pomeron, we will
want to measure the dijet cross section as well as the cross section for
other process, such as diffractive W boson
and diffractive b quark production.
These processes have different dependences on the quark and gluon content
of the pomeron, as well as the pomeron structure function. Measuring
the cross section thus gives complementary information to that obtained
from various angular and kinematic distributions. An example of the
power of the cross section to distinguish between different pomeron models
is the measurement of the dijet cross section for two jets with ![]() GeV.
The prediction for a hard gluon cross section is 2.3
times the hard quark cross section, with little
GeV.
The prediction for a hard gluon cross section is 2.3
times the hard quark cross section, with little ![]() or
or ![]() dependence,
while the soft gluon ranges from about 0.5 to 3.0 times
the hard gluon depending on the exact
dependence,
while the soft gluon ranges from about 0.5 to 3.0 times
the hard gluon depending on the exact ![]() and
and ![]() cuts.
From our experience in Run I, we expect to be able to measure
this cross section with a better than 50% error. If we have enough
statistics to raise the
cuts.
From our experience in Run I, we expect to be able to measure
this cross section with a better than 50% error. If we have enough
statistics to raise the ![]() threshold, the error can be reduced to
about 30%.
threshold, the error can be reduced to
about 30%.
There are currently no double pomeron Monte Carlos, but we are working on modifying POMPYT to simulate hard double pomeron exchange. Jon Pumplin and John Collins also are interested in incorporating their double pomeron models into Monte Carlos and we expect to have more and better predictions over the next couple of years. The final word will of course be given by the unique data samples obtained with the FPD.