with the optical theorem
and the relation
 to obtain
to obtain
where
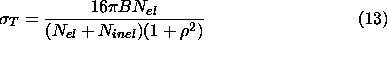 is the extrapolated number of elastic events,
is the extrapolated number of elastic events,
The luminosity independent method [46] is the best way to
measure the total cross section using the FPD, since it does not require
very low |t| acceptance. This method combines the definition of the total
cross section (Eq. 11)
![]()
with the optical theorem
![]()
and the relation  to obtain
to obtain
![]()
where 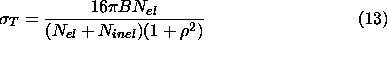 is the extrapolated number of elastic events,
is the extrapolated number of elastic events, ![]() is the number of inelastic events, B is the slope of the elastic |t|
distribution,
and
is the number of inelastic events, B is the slope of the elastic |t|
distribution,
and ![]() is the ratio of the real to imaginary
part of the elastic scattering amplitude.
is the ratio of the real to imaginary
part of the elastic scattering amplitude.
In a low luminosity special run with extra beam scraping, it will be
possible to obtain a ![]() GeV
GeV![]() .
CDF and E710 are in very
good agreement for the elastic slope
in the region |t|<0.15 GeV
.
CDF and E710 are in very
good agreement for the elastic slope
in the region |t|<0.15 GeV![]() (
(![]() ), with a virtually
identical central value yielding a world average measurement of
), with a virtually
identical central value yielding a world average measurement of
![]() GeV
GeV![]() .
For a 50,000 event special run, the largest
error in the measurement should be about 1.5%
from the extrapolation to t=0.
The contribution of the
.
For a 50,000 event special run, the largest
error in the measurement should be about 1.5%
from the extrapolation to t=0.
The contribution of the ![]() error
to the cross section is small, and the Level Ø counters will be
used to accurately measure
error
to the cross section is small, and the Level Ø counters will be
used to accurately measure ![]() . The slope in the region
0.15<|t|<0.6 GeV
. The slope in the region
0.15<|t|<0.6 GeV![]() (
(![]() ) is flatter than
) is flatter than ![]() ,
and is measured to be
,
and is measured to be ![]() GeV
GeV![]() [46]. This
3% error could be reduced to about 0.5% during this run.
[46]. This
3% error could be reduced to about 0.5% during this run.
The elastic cross section is roughly 20 mb, and about 8%
of the events have |t|>0.15 GeV![]() , giving an effective cross
section of 1.6 mb. Assuming a
, giving an effective cross
section of 1.6 mb. Assuming a ![]() acceptance of 20% and a
luminosity of
acceptance of 20% and a
luminosity of ![]() cm
cm![]() gives a rate of 3 Hz.
A five hour run will thus give 50,000 elastic events.
Note that this will be a one-time run which could be done after
all of the properties of the
FPD are well-understood, and would consequently not require any
dedicated setup time.
With a data sample of 50,000 good elastic events
it should be possible to measure the total
cross section to an accuracy of about 2%.
gives a rate of 3 Hz.
A five hour run will thus give 50,000 elastic events.
Note that this will be a one-time run which could be done after
all of the properties of the
FPD are well-understood, and would consequently not require any
dedicated setup time.
With a data sample of 50,000 good elastic events
it should be possible to measure the total
cross section to an accuracy of about 2%.